The circle of fifths just blew my mind
May 7th, 2012 at 6:17 pm (Mathematics, Music)
In tandem with violin practice, I’m working my way through Practical Theory Complete: A Self-Instruction Music Theory Course. It starts out REALLY basic, with simple notation and rhythms, but works all the way up to composing your own song (!). I just hit lesson 39 (of 86) and my brain exploded.
I’d heard about the “circle of fifths” before, but had never delved into what it actually meant. What it provides is a nifty arrangement of the various (major) keys, anchored by the key of C, that reveals patterns in the progression of sharps and flats that comprise each key’s signature. Check out this awesome magic:
Starting from the key of C, if you go up a fifth, you reach G. The key of G introduces one sharp, F#. Up another fifth from G, you get D, which in addition to F# also features C#. And so on. (The order of keys G-D-A-E are easy to remember for violin players, since those are the four fifth-separated strings on the instrument.) Going down from C a fifth, you get F. The key of F introduces one flat, B♭. Down another fifth is the key of B♭, which adds E♭. And so on.
This defines a linear relationship between C and the keys “above” it as well as “below”; but positioning them on a circle reveals a bit more of the magic: three of these keys are redundant (or “enharmonic”: they sound the same but are notated differently). This diagram shows that G♭ and F# are the same key; my workbook’s diagram also shows that D♭ and C# are enharmonic, as are C♭ and B. And hey, look on any keyboard and what do you see? These key pairs are, in fact, literally the same key.
Want more magic? What’s going on here is modular arithmetic! Not mod 7, but mod 13: the set of values includes { C, C#, D, D#, E, F, F#, G, G#, A, A#, B, B#, C }. For each key, the major scale is traditionally given as WWHWWWH, where W = “whole step” and H = “half step”. But let’s instead view a scale starting on x as the sequence
So the key of C contains { C, D, E, F, G, A, B, C }; C+12 = C in this modular land. Now if we go up a fifth and examine the key of G, that’s the same as adding 5 to all entries. The key of G is therefore
{ G, A, B, C, D, E, F#, G } after doing the addition mod 13.
That is, it’s as if we jumped 5 items forward, but then the extra whole-step in the second tetrachord threw off the pattern and caused the F to become an F#. If you move on to the key of D, the first four notes again are unchanged (with respect to the key of G): { D, E, F#, G }, but then we have to shift one note in the second tetrachord again, yielding { A, B, C#, D }. In this way, the sharps keep building on themselves, and the new sharps introduced in each key alternate. The sharp order is F#, C#, G#, D#, A#, E#, B# (see the pattern?). A similar process explains the progression of flats going “down” from C.
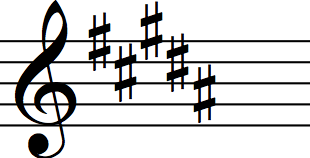This relationship seems also to explain the conventional structure in how key signatures are written. The key of B major has five sharps, which are C#, D#, F#, G#, A# if you write them in ascending order, but F#, C#, G#, D#, A# if you write them in this circle-of-fifths-inspired order. And that seems to be just what one does (see right).
Patterns! Math! Music! And of course, at the heart of this magic is… physics. :)
David said,
May 7, 2012 at 7:01 pm
Hmmm …. has someone been doing a lot of work for the crypto class that involves modular arithmetic? :-P
With your new fascination, you’ll probably enjoy the following:
https://www.facebook.com/photo.php?fbid=341568569198206&set=a.207042772650787.61098.207019572653107&type=1&theater
And one typo, if I may: “The key of B major has five *sharps*” (knowledge of which you of course demonstrate both subsequently and previously).
Terran said,
May 7, 2012 at 7:10 pm
Ah right! Did I ever share with you my essay on a similar insight?
A more recent revelation: the basic chord structure is 1-3-5 (e.g., C-E-G or Bb-D-F). The reason that’s a chord, it appears, is that modern western instruments are generally tuned in Equal temperament — that is, adjacent notes differ by a constant frequency factor, yielding a logarithmic frequency spacing as you go up the (chromatic) scale. An octave is a frequency doubling, so every half-step is a twelfth-root of two frequency multiple up. In this tuning, the “3” note (i.e., two whole steps or four semitones up from the tonic) turns out to be very close to a frequency ratio of 1.25 (2^(4/12)~=1.2599). Similarly, the “5” note (three and a half steps or seven semitones) is very close to a frequency ratio of 1.5 (2^(7/12)~=1.4983). Both 1.25 (5/4) and 1.5 (3/2) are resonant frequency relationships. So that’s (part of) why those notes “sound good” when played together.
David said,
May 7, 2012 at 7:23 pm
Terran, you’re probably also aware that in olden days, tuning was actually precisely by a factor 1.5 for the fifths. As you keep that up over the fifths, you’ll eventually sound quite out of tune. “Well-tempered” tuning tried to remedy that, and Bach appeared to have been an early advocate. (Though real enthusiasts assert that “well-tempered” is actually not the same as “same multiplicative increments”.)
Kiri said,
May 7, 2012 at 8:45 pm
David, yes, the crypto class primed me. :) Thank goodness music theory doesn’t require solving things like x2 – 7x + 3 = 1 in Z13! Also, thanks for the correction about B major — fixed.
Terran, cool stuff. My violin teacher claimed that people “used to” think thirds sounded bad, but now we think they sound good. I’m not sure how far back in history she’s thinking. I’d expect resonance to sound good no matter the century. But maybe that’s over-simplifying the human ear. Obviously there are current cultures who enjoy chords that “we” find quite dissonant.
David, is that why my violin teacher insists that I should tune my strings to be perfect fifths apart, even if they then disagree with my tuner? She just said that if I tuned them independently (against the tuner), the result would “not be in tune,” and I didn’t get to follow up.
Kiri said,
May 7, 2012 at 8:47 pm
By the way, David, that link is SO COOL! I may have to print it out and post it on my door at work.
David said,
May 7, 2012 at 10:21 pm
Tuning in perfect fifths: Yes, that’s probably the reason. It’s also why you should only tune one string from the piano when you play together.
Link: I thought you might like it. I found it via a Facebook post from my friend Martin Giese (who is an accomplished guitar player).
Thirds: That would be about the 13th/14th century. At the time, most music was just using parallel fifths/octaves. By the 16th century, writing music that uses fifths moving in parallel was considered creating strange/undesirable sounds. In particular, when counterpoint is taught in the mold of Palestrina (one of the main representatives of the 16th century style of choral writing), having voices move in the same direction in 5ths is a big no-no. That holds all the way into the mid-18th century, at least, and is still how things are taught in intro classes.
3rds are definitely less consonant than 5ths, but for the same reason add some richness to the sound. Apparently, that was too much for the desired purity (and text intellegibility) of 14th century church music. I remember a joke among counterpoint geeks which basically goes: “Counterpoint lesson from Perotin: [in stern voice]: ‘Those were parallel thirds, young man!'”
(If you take an intro counterpoint class, you can often find big red markings on your homework for writing parallel *fifths*.)
Anyway, enough rambling …
Leigh Torgerson said,
May 8, 2012 at 8:38 am
7th grade woodwind class taught us order of sharps = “Fat Cows Get Dumpy After Eating Berries” and order of flats was something like “Boys Eat Apple Dumplings Get Cramps Fast”.
So, I recommend you read “How Equal Temperment Ruined Harmony” by Ross W. Duffin. Will loan it to you if you like!
Kiri said,
May 27, 2012 at 11:10 am
I came in for my next lesson all excited about the circle of fifths, and my violin teacher picked up on that and we had a nice impromptu discussion, although it didn’t go beyond what’s here. She taught me “Fire Causes Great Damage Always Ever Beware” for the sharps, and for the flats “B-E-A-D Go Call Fred” — or of course it’s just the sharp order, reversed. I’ll have to share Leigh’s mnemonics with her, too!
Matteah said,
April 19, 2015 at 7:49 pm
Btw, there’s another mnemonic you can remeber
Flats: Battle Ends And Down| Goes Charles’s Father
Sharps: Father Charles Goes Down| And Ends Battle
Kate said,
August 16, 2023 at 12:24 am
I’m assuming I’m starting this as I’m on grade 4 violin, I just wondered what the inner circle is compared to the outer circle ( I’ve got number dyslexia, I can’t rememb the medical term for it) but it takes me much longer to understand things to do with numbers and maths.
Thanks for any help ????